problemas propuestos
sobre electricidad
Un cilindro infinito de radio a,
tiene una carga por unidad de volumen
. Demuestre que el
potencial a una distancia r del eje del cilindro está dado por:
y
Un
condensador de placas cuadradas, cada una de lado a, forma un ángulo q entre sí, tal como se muestra en
la figura.
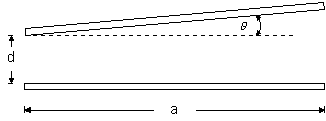
Demostrar
que para valores pequeños del ángulo q, la capacitancia
del sistema, está dada por:
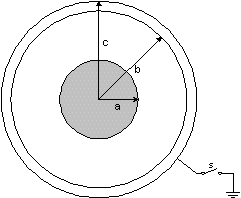
Una
distribución uniforme y volumétrica de carga eléctrica de densidad ro, limitada
por una esfera de radio “a”, es colocada en forma concéntrica, dentro de
un cascarón conductor esférico-hueco de radios interior “b” y exterior “c”,
tal como se muestra la figura. Dicho
cascarón, se encuentra conectado a tierra a través de un interruptor “s”. Determinar el potencial electrostático en
todos los puntos y las densidades de carga sobre cada una de las superficies
del cascarón esférico, tanto para cuando “s”, está abierto, como para
cuando “s”, está cerrado.
Determinar
el campo eléctrico producido por la siguiente distribución de carga:
y 
Para
almacenar energía eléctrica, se utiliza un sistema conformado por una batería
de 5,000 condensadores, conectados en paralelo, cada uno de ellos con una
capacitancia de 5 mF. ¿Cuanto costaría cargar esta batería hasta
50,000 voltios, suponiendo que la tarifa que impone la empresa
distribuidora de energía eléctrica, es de 6 ¢/kWh?
En el
centro de un conductor esférico hueco e inicialmente descargado, de radio
interior a y exterior b, se coloca una partícula puntual positiva
de carga q. Determinar el
potencial eléctrico en todos los puntos y obtener su comportamiento matemático.
Considérese
que en alguna región del espacio, existe un campo eléctrico que cumple con la
siguiente relación:
¿El campo
eléctrico anteriormente indicado, es conservativo?, ¡demuéstrelo entonces!. Determine la expresión del potencial
electrostático en todos los puntos, y, calcule la carga total contenida dentro
de un cubo definido por: 
, 
, 
, donde todas las dimensiones espaciales, se han expresado en
[cm].
Un cable
concéntrico con envoltura exterior de plomo, tiene un conductor de cobre de
0.50 [cm] de diámetro, el dieléctrico tiene un espesor de 0.15 [cm] y cuyo
coeficiente es 1.88; el cable se garantiza para operar a 8.00 [kV]. Calcular la carga de 1 [km] del cable cuando
tiene aplicada la diferencia de potencial de garantía.
Dos capacitores
de 1 y 2 [mF]
respectivamente, se conectan en serie a una diferencia de potencial de 600
[V]. Calcular la carga eléctrica que se
almacena en cada capacitor. Si se desconectan con carga y se conectan en
paralelo con las placas de igual polaridad juntas, determinar la diferencia de
potencial a la que estará el referido banco de capacitores.
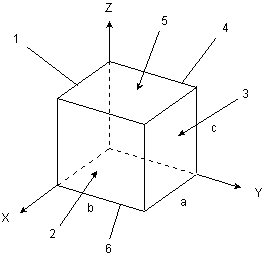
El bloque de material dieléctrico mostrado en la
figura, se encuentra permanentemente polarizado, y su campo de Polarización
varía según la relación matemática:
|
|
donde |
Considerando que: la cara 1, se encuentra contenida
en el plano XZ, la cara 2, es paralela al plano YZ, la cara
3, es paralela al plano XZ, la cara 4, se encuentra contenida
en el plano YZ, la cara 5, es paralela al plano XY y la cara
6, se encuentra contenida en el plano XY. Adicionalmente, en el interior de este paralelepípedo se han distribuido
cargas libres en su volumen y con una densidad volumétrica:
Determinar las distribuciones de cargas de polarización
(DCP). Considerando la respuesta
anterior, encontrar la carga total del sistema.
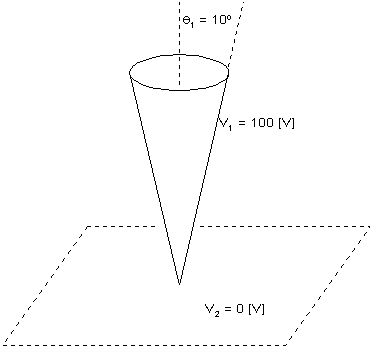
Para la disposición de las superficies conductoras que se muestra
en la figura, determinar la distribución de carga sobre los planos conductores
en q2 = p/2.
Una corriente eléctrica cruza la superficie plana que separa dos medios. (a) Si la dirección de la corriente en el medio 1 forma un ángulo de 40º con la normal, determinar el ángulo que forma la corriente en el medio 2 con la normal. (b) Si la densidad de corriente en el medio 1 es de 1 [A/m2], determine la densidad superficial de carga libre (real) que se acumula en la interfase.
Considérese que: s1
= 10 [S/m], e1
= e0, y, s2 = 1 [S/m], e2 = 4 e0.
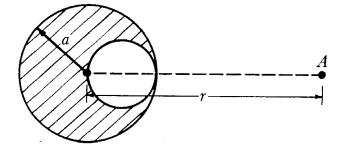
Una esfera no conductora de radio “a” con una
densidad de carga uniformemente distribuida r tiene una cavidad esférica tal como se muestra en la figura. Determinar la intensidad de campo eléctrico
en el punto A.
Obtener la
ecuación que nos permita determinar la resistencia del forro aislante de un
conductor cilíndrico (resistencia de fuga) y con esta ecuación calcular la
resistencia de fuga de un kilómetro de alambre número 6 AWG con forro de hule,
cuyo espesor de 0.25 [pulg.] y r = 1014
[W-cm]. El
diámetro del alambre número 6 es de 0.162 [pulg.].
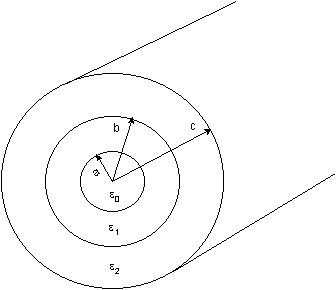
Se tiene tres superficies conductoras de radios a, b y c,
con densidades de carga libre sa,
sb, y sc respectivamente. El
espacio entre cilindros está lleno con dieléctricos cuya permitividad se
especifica en el gráfico. Considérese
que: a = 3 [m], b = 4 [m], c = 5 [m], sa = 8 x 10-9
[C/m2] y sb = -12 x 10-9 [C/m2], adicionalmente
los materiales dieléctricos tienen permitividades: e1
= 2 e0 y e2 = 3 e0. Bajo estos
parámetros, ¿Cuál debe ser el valor de sc para que |D(r>c)| sea nulo?
