![]()
problemas propuestos
sobre magnetismo
![]()
Un
cilindro de cobre, infinitamente largo y de radio a, transporta una corriente I, la misma
que no se encuentra uniformemente distribuida, sino que su densidad de
corriente eléctrica cumple con la relación:
J=Ar3, donde A es una constante positiva
y r, es distancia desde el eje del cilindro a cualquier punto dentro del
mismo. Determinar la densidad de campo
magnético en todos los puntos.
El freno
electromagnético de corrientes parásitas o de Foucault, consiste
básicamente en un disco de conductividad s y de
espesor t, que gira alrededor de un eje que pasa por su centro simétrico,
en presencia de una densidad de campo magnético B, aplicado en
forma perpendicular al plano del disco y sobre una superficie pequeña de área a2. Si el área a2 se localiza
a una distancia r del eje del disco, encontrar aproximadamente la
expresión del momento que tiende a disminuir la velocidad del disco, en el
instante en el cual el disco gira a velocidad angular w.
Este es el principio básico de frenado, que se utiliza en los medidores
de energía eléctrica para evitar el deslizamiento del disco, una vez que la
carga conectado es nula.
Un campo
magnético uniforme, cambia de manera que dB/dt = constante. Considérese un volumen V de cobre,
utilizado para formar un toroide de sección circular de radio a y el
radio de la espira de radio b.
Demostrar que la corriente que produce la densidad de campo magnético en
el toroide, no depende de las dimensiones a y b, y cumple con la
siguiente relación:
![]() , donde r es la
densidad del cobre.
, donde r es la
densidad del cobre.
Sobre un
solenoide de sección transversal circular de radio R, Na
espiras y longitud la, se devana un segundo solenoide
de Nb espiras y longitud lb, (donde lb<la). Asumiendo que ambos devanados son muy largos
con relación al diámetro común de los mismos, y, despreciando el efecto de los bordes,
determinar la inductancia mutua Mab y Mba. Asuma que el material sobre el cual se
devanan ambos solenoides, posee una permeabilidad m.
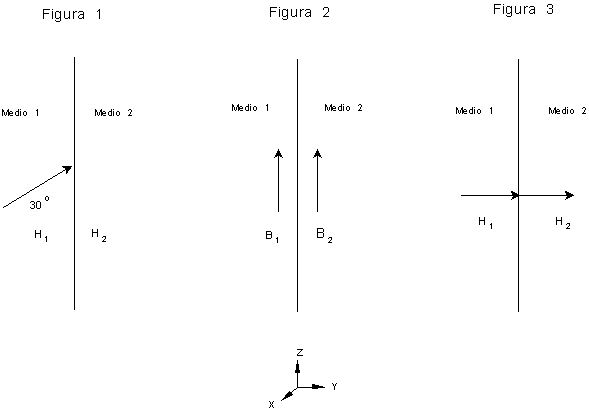
Considerar para todos los casos que: m1
= 5 m2. (a) En la Figura
1, se aprecia la interfase entre dos medios cuyas permeabilidades magnéticas
son m1 y m2 respectivamente. La
superficie de separación es perpendicular al eje Y empleado en el sistema
cartesiano ilustrado. Si se conoce la
existencia de un campo H de magnitud 500 A/m que está incidiendo
oblicuamente y a 30o con respecto a la horizontal desde el medio 1,
¿con qué dirección sale el campo en el otro medio?
(b) Ahora supóngase que el campo magnético apunta en la
dirección Z, tal como lo muestra la Figura 2.
¿Qué relación existe entre B1 y B2?
(c) Por último, supóngase que el campo magnético existe
paralelo al eje Y, tal como lo muestra la Figura 3. ¿Qué relación existe entre H1 y H2?
Se tiene
un condensador de placas planas paralelas circulares de radio R = 5
[cm], considerando que en el interior del mismo la rapidez de variación del
campo eléctrico es de 1012 [V/m-seg], determinar el valor el de la
corriente de desplazamiento, y, demostrar que es idéntica a la corriente de
conducción.
Demostrar
que si el flujo magnético que pasa por una bobina de N espiras, cambia
de F1 a F2, entonces la carga que pasa por el circuito de resistencia
total R, está dada por:
![]()
Por una
esfera hueca de radio R, construida en material conductor, circula una
corriente eléctrica de intensidad I = constante. Determinar la intensidad de campo magnético H
para todos los puntos interiores y exteriores de la esfera conductora.
Se nos ha propuesto el diseño de una línea de transmisión
superconductora, con las siguientes características: Transportará 108
[kW] a 200 [kV – DC] sobre una distancia de 103
[km]. Los conductores tienen sección
transversal circular de 5 [cm2] y están separados por 5
[cm] de eje a eje. (a) Calcular el valor
de la fuerza por unidad de longitud sobre cada uno de los conductores. (b) Determinar la inductancia de esta línea
de transmisión.
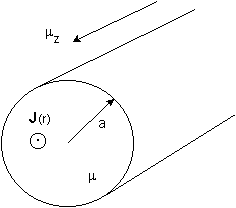
Un cilindro conductor recto e infinitamente largo de radio “a”
transporta una densidad de corriente distribuida en su sección transversal, que
cumple con la siguiente relación:
![]()
La permeabiliad del cilindro conductor es igual a 500 m0. Determinar las distribuciones de las
corrientes de magnetización (DCM).
Un toroide de hierro fundido, sección de 2 pulg.2
y 15 pulg. de longitud, tiene intercalado un entrehierro de 0.2 pulg. de
longitud y 4 pulg.2 de sección transversal. Suponer que la electromotanza que se aplica
a la bobina de 1,000 espiras y 5 W
de resistencia eléctrica es de 15 voltios, determinar el flujo magnético que
circulará en dicho circuito.
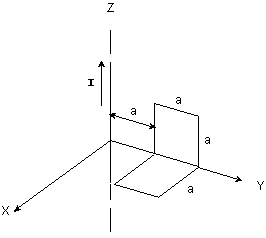
Un alambre conductor recto e infinitamente largo, transporta
una corriente I constante, que circula coincidentalmente con el eje de las
“z”, tal como se muestra en la figura.
Una espira rectangular de dimensiones a x 2a se dobla en ángulo
recto y es colocada a una distancia “a” del alambre.
Determinar:
a)
El flujo magnético
que atraviesa la espira.
b)
Supóngase ahora que la
corriente varía con respecto al tiempo, de tal manera que cumple con la
relación: I(t)
= I0 (1 - e -t/t). Encuentre y grafique en función del tiempo
la fem inducida en la espira, considerar t = constante.
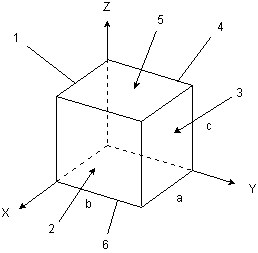
El bloque de material ferromagnético mostrado en la figura,
se ha magnetizado según la relación:
![]()
Considerando que: la cara 1, se encuentra
contenida en el plano XZ, la cara 2, es paralela al plano YZ,
la cara 3, es paralela al plano XZ, la cara 4, se
encuentra contenida en el plano YZ, la cara 5, es paralela al
plano XY y la cara 6, se encuentra contenida en el plano XY. Determinar las distribuciones de corriente
de magnetización.
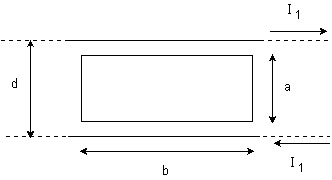
Un lazo conductor, de dimensiones a x b, reposa en el
plano de dos alambres paralelos muy largos, simétricamente colocados. Por los conductores largos circula una
corriente I1, en sentidos
contrarios, tal como se muestra en la figura.
Calcular el coeficiente de inductancia mutua entre el lazo y los
conductores largos (proporcionar su respuesta en función de las dimensiones
señaladas).
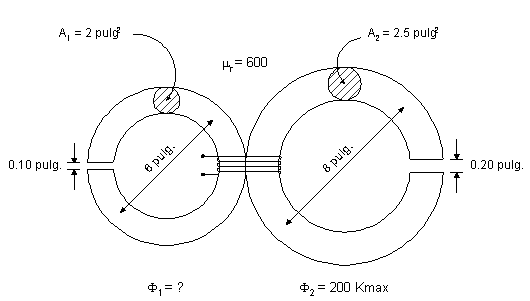
Para el circuito magnético
que se muestra en la figura, determinar el flujo que pasa por el entrehierro de
la izquierda y la corriente necesaria en la bobina de 400 espiras, para
producir un flujo de 200 Kmax en el entrehierro de la derecha.
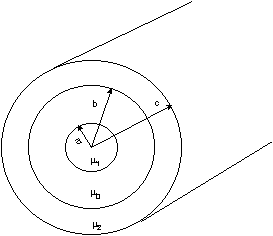
Un conductor muy largo de radio a y permeabilidad m1, transporta
una corriente estacionaria de intensidad I. Coaxialmente con el conductor, es colocado
un tubo de permeabilidad m2 con radio
interior b y radio exterior c, tal como se muestra en la figura.
Determinar el campo M
y las Distribuciones de Corrientes de Magnetización (DCM), en todos los puntos.